Here’s a great quote from a recent Wall Street Journal article:
"Events that models only predicted would happen once in 10,000 years happened every day for three days." Matthew Rothman, Ph.D., Lehman Brother Holdings
I hate to take pot shots at analytical guys–I’m one myself. After all, you don’t go to graduate school in economics just to pick up chicks. (Well, that’s one reason among many.)
Let’s ask, how could they be so wrong? Simple. They were not remembering their assumptions.
Remember the normal curve (also called the bell shaped curve)? It looks something like this (courtesy of Wikipedia):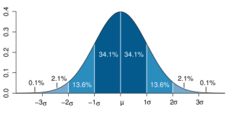
Suppose we have a bunch of data, like on daily prices. (More likely, on the change in the logarithm of the price.) We can look at the data and see if it fits the normal curve. But wait. We don’t have many observations out at the tails of the curve. Like things that should occur once every 10,000 years. We may not have any observations, or we may have one. In any event, we can’t really tell if the tails of the distribution fit the normal curve or not. So we look at the great mass of data in the middle, say that it looks like it fits the normal curve, then assume that the tails of the normal curve also fit the data.
But they don’t. We’ve known for years that financial transactions are "leptokurtic," which is a great way of saying they have fat tails. In other words, there are more extreme values than the normal curve would predict. I assume that Dr. Rothman knew that, but what does one do with the knowledge? Assume some other distribution, similar to the normal curve, but with fat tails. Unfortunately, it’s very hard to know just how fat the tails really are. We can collect many, many years of data and still not know very much about the far tails of the distribution.
Great example: In 1997, my local newspaper reported that the Tualatin River (near my home) had surpassed the hundred year flood mark, but "it wasn’t as high as last year’s flood."
What’s the moral of this story? We have to be very cautious about extreme events. We don’t really have a clue how frequent they are. That’s true of financial markets, but also true of physical sciences. If an engineer tells you the boiler has one chance in 10,000 of blowing up, I’ll bet that the engineer does not really know the true odds–he’s just extrapolating on the assumption that the distribution is nice and neat.
What to do about it? Don’t place too much confidence in hedging strategies. Instead, plan for bad events, and be sure that you know how to react when they happen.


